【BlenderとPython】単振動のアニメーション
BlenderとPython(bpy)を使ってアニメーションを作ってみたかったので単振動に挑戦しました
導出
摩擦や空気抵抗がない時、ある一つの物体が安定な平衡点の近くで行う運動
例:ばねにつるされた重りの運動
直線上を運動する質量mの物体について
x軸上を運動すると考える
物体は原点からの距離に比例する力を受けるとする
ばねにつるされた物体について考えるときkはばね定数
$$F=-kx$$
運動方程式を用いる
$$F=ma$$
よってこの時の運動方程式は
$$m\frac{d^2x}{dt^2}=-kx$$
移項して計算すると
$$\frac{d^2x}{dt^2}+\frac{k}{m}x=0$$
ここで角振動数を用いる
$$\omega_0=\sqrt{\frac{k}{m}}$$
よって
$$\frac{d^2x}{dt^2}+\omega_0^2x=0$$
これは2階の斉次線形微分方程式なので解の形は次になります
$$x=e^{\lambda t}$$
これを代入して
$$(\lambda^2+\omega_0^2)e^{\lambda t}=0$$
よって
$$(\lambda^2+\omega_0^2)=0$$
$$\lambda=\pm i \omega_0 $$
解は
$$x=e^{i\omega_0 t}$$
$$x=e^{-i\omega_0 t}$$
2階の斉次線形微分方程式の一般解は2つの解の線形結合になるので
運動方程式の解は次になります
$$x=C_1 e^{i\omega_0 t}+C_2 e^{-i\omega_0 t}$$
オイラー公式を用います
$$e^{i\omega_0 t}=\mathrm{cos}{\omega_0 t}+i\mathrm{sin}{\omega_0 t}$$
$$e^{-i\omega_0 t}=\mathrm{cos}{\omega_0 t}-i\mathrm{sin}{\omega_0 t}$$
よって
$$x=C_1(\mathrm{cos}{\omega_0 t}+i\mathrm{sin}{\omega_0 t})$$
$$+C_2(\mathrm{cos}{\omega_0 t}-i\mathrm{sin}{\omega_0 t})$$
$$x=(C_1+C_2)(\mathrm{cos}{\omega_0 t})+i(C_1-C_2)\mathrm{sin}{\omega_0 t})$$
ここで
$$B_1=C_1+C_2$$
$$B_2=i(C_1-C_2)$$
とすると次の式になる
$$x=B_1\mathrm{cos}{\omega_0 t}+B_2\mathrm{sin}{\omega_0 t}$$
ここで三角関数の合成公式を用いる
$$a\mathrm{sin}{\theta}+\mathrm{cos}{\theta}=\sqrt{a^2+b^2}\mathrm{sin}({\theta+\alpha})$$
よって一般解を次のように書くことができる
$$x(t)=A\mathrm{sin}({\omega_0 t+\alpha})$$
また、この運動の周期は
$$f=\frac{2\pi}{\omega_0}$$
$$T=\frac{1}{f}=\frac{2\pi}{\omega_0}$$
BlenderとPython(bpy)
位置の時間変位を「Cube1」
単振動を表現する球を「Cube2」
円上を等速運動する「Cube3」をy軸に射影したものが「Cube1」である
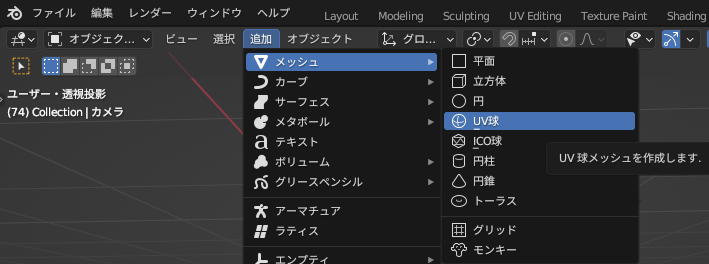
Cube1,2,3をBlenderで「追加」→「メッシュ」→「UV球」から作成
それぞれ名前を付ける
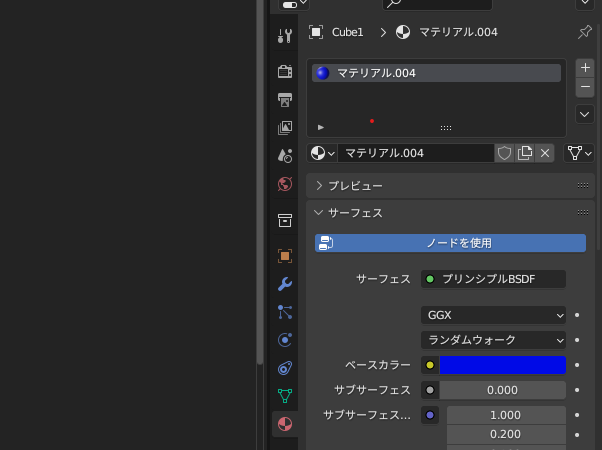
それぞれの球に「マテリアル」から「ベースカラー」を選択し色を付ける
x軸,y軸,z軸はお好みで作成してください
角振動数の単位はrad(ラジアン)なので次の式を用います
$$\mathrm{rad}=\frac{2\pi}{N}t$$
フレーム数は自由に変更してください
Blenderの「Scripting」→「新規」からテキストエディタを表示できます
右にある「▶」をクリックすると実行できます

#bpyとmathを使えるようにする
import bpy
import math
#開始時の座標を指定する
start_pos = (0,0,0)
#変数obに3D viewportにあるオブジェクトを代入する
ob1 = bpy.data.objects["Cube1"]
ob2 = bpy.data.objects["Cube2"]
ob3 = bpy.data.objects["Cube3"]
#分割数を入力
N=12
#開始のフレームを指定する
frame_num = 0
#目標の座標に移動する処理を繰り返す
for i in range(N+1):
rad = 2* math.pi * i /N
#それぞれ球の位置を求める
p1=(0,i,math.sin(rad))
p2=(0,0, math.sin(rad))
p3=(0,math.cos(rad), math.sin(rad))
#開始のフレームを設定する
bpy.context.scene.frame_set(frame_num)
#変数locationに目標の座標の値を代入する
ob1.location = p1
ob2.location = p2
ob3.location = p3
#キーフレームの挿入を行う
ob1.keyframe_insert(data_path = "location",index = -1)
ob2.keyframe_insert(data_path = "location",index = -1)
ob3.keyframe_insert(data_path = "location",index = -1)
#フレームを10ずらす
frame_num += 10まとめ
単振動の解を出し、bpyを書き、Blenderを操作しアニメーションをレンダリンング
結構時間がかかり苦労しました
今回は動かすことに主力を置いたため、数式など理論に不適切な点があるかもしれません
軸や着色、ライティング、レンダリンングなど今後は工夫したいと思います